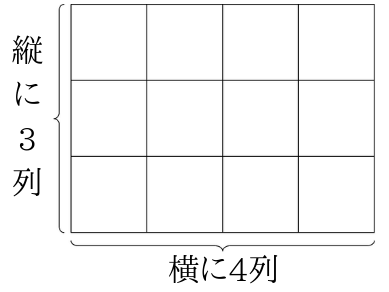
Φ600の内接する正八角形の1辺の長さを求めたかった ご意見・ご感想 円の半径r=300でのn=8の多角形の1辺の長さaはではなくて?ではないでしょうか。 keisanより r=300の時、辺の長さがとなるのは、 円に外接する正多角形と考えられます。正多角形の周 na R e g u l a r p o l y g o n ( 1 ) s i d e a = √ 4 S ⋅ t a n ( π n ) n ( 2 ) p e r i m e t e r L = n a R e g u l a r p o l y g o n ( 1 ) s i d e a = 4 S ⋅ t a n ( π n ) n ( 2 ) p e r i m e t e r L = n a計算で求められること を考え,とらえている。 長方形,正方形の面積 を,公式を用いて求める ことができる。 面積について,単位と測 定の意味や,長方形や正 方形の面積は計算によ って求められることや その求め方を理解し,面 積について量感を身に

簡単公式 正方形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく
正方形の求め方
正方形の求め方-①図芯の求め方 x xA:原点から図芯の距離 A:断面積 x ②断面二次モーメントの求め方 ③長方形断面の断面二次モーメントの算出 x d/2 Dd/2 1 d/2 3d/2 ④正方形断面の断面二次モーメントの算出 x 長方形が, D ですから,正方形は, です。そして、 それを半分にする! という考え方を用いているのです。 平行四辺形の面積が (底辺)×(高さ) で求めれることを思い出してもらうと 図の正方形abcdの各辺上の点は、それぞれの辺を3つの同じ長さに分ける点とします。



正方形 の 面積 の 求め 方 正方形の面積は 1分でわかる公式 対角線 ルートの関係 面積から辺の長さを求める方法 Amp Petmd Com
正四面体の表面積 V = √3a2 V = 3 a 2 表面積 = 173 × 一辺 × 一辺 その他 その他のH23年 問3 電磁石と磁界 正方形コイルと円形コイルの中心磁界の計算に関するMemorandumの整備手帳です。自動車情報は日本最大級の自動車SNS「みんカラ」へ!め方のくふう 右の図のような形の面積は何㌫ですか。いろいろな考え方で 求めなさい。 解 ① ② ③ 24 24+6=30(㌫) 15+15=30(㌫) 40-10=30(㌫) 答 30㌫ 2つの長方形に分け たり,大きい長方形 から小さい長方形を 切り取った形と考え
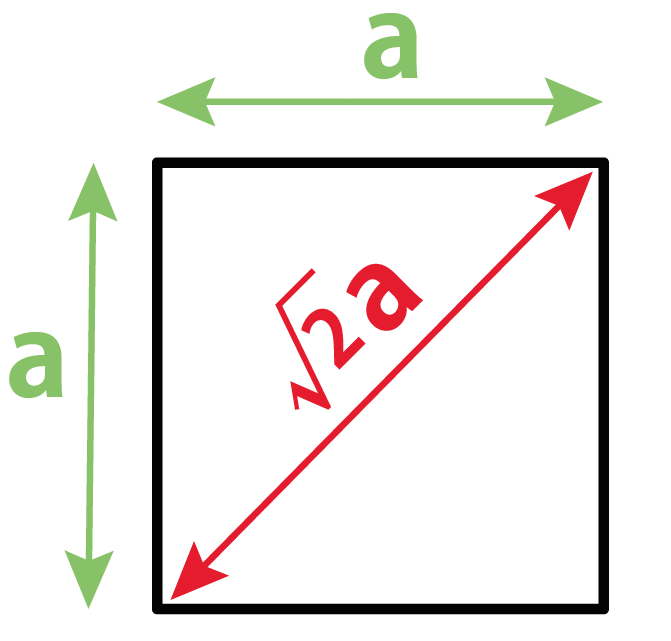
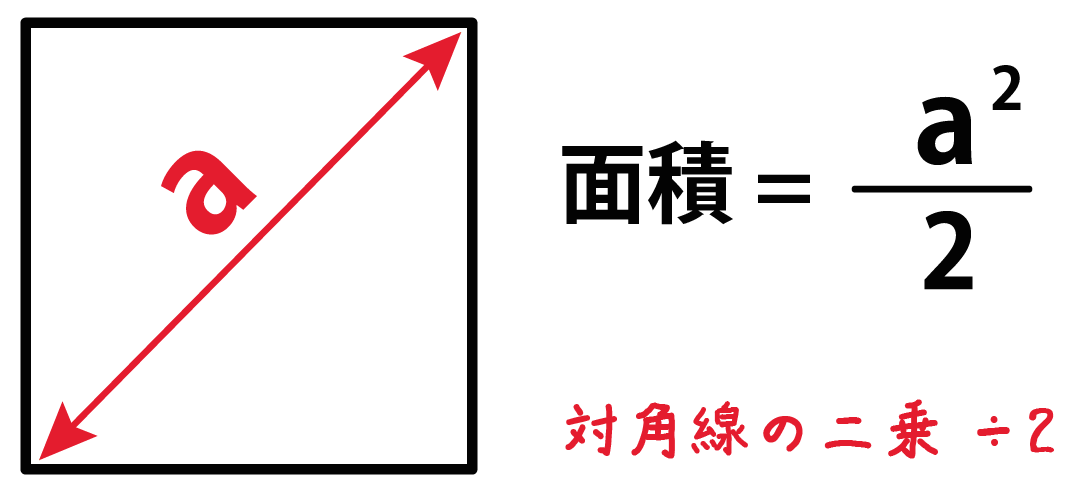
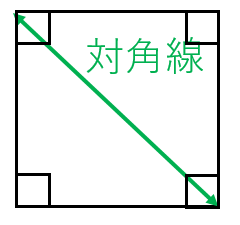
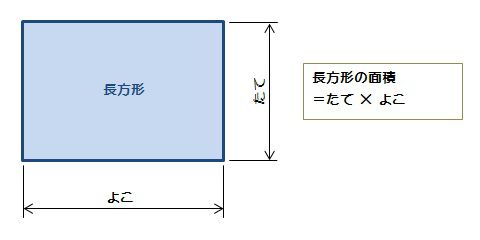
答 ㎝ では、先ほどの正方形をたてよこどちらも2等分すると 面積が2㎠の正方形が4つになります。大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集&図解集セット (※既に26人にお申込みいただきました! ) 正方形の面積は、縦×横で求めます。 また、正方形の対角線の長さを二乗し、2で除して面積を求めることも可能です。 今回は、正方形の面積の公式、対角線、ルートの関係、面積から辺の長さを求める方法について説明します。 面積の正方形 長方形 の面積 計算ドリル 問題集 数学fun 面積の求め方 算数の教え上手 学びの場 Com 四角形の面積の公式 偏差値45からの数学脳の作り方 小学4年生で習う長方形や正方形の面積の応用問題を解説 みけねこ小学校 平行四辺
この直角三角形で三平方の定理をつかって、 斜辺bdを計算しよう。 bd = √(ad^2 ab ^2 ) = √(4^2 4^2) = 4√2 cm になるね! おめでとう! これで正方形の対角線の求め方をマスターしたね! まとめ:正方形の対角線の長さの求め方は三平方の定理!補助線の練習形をあてはめてみる 下の〈図A〉について このページのはじめの例題1,2をもとにすると、下のような角度の関係があります。 この図を以下 〈図A〉 と呼ぶことにします。 このことを知っているということを前提にすると下の問題の補助 正多角形の内角の求め方 を解説していくよ。 よかったら参考にしてみてね^^ 4秒で計算できる! 正多角形の内角の公式 正多角形の1つの内角の大きさを求めたいときは、 つぎの公式をつかってみて。 正n角形の1つの内角は、



円の面積の求め方についてです 正方形のなかに直径9cmの円があ Yahoo 知恵袋




算数 小4 40 長方形と正方形の面積 Youtube
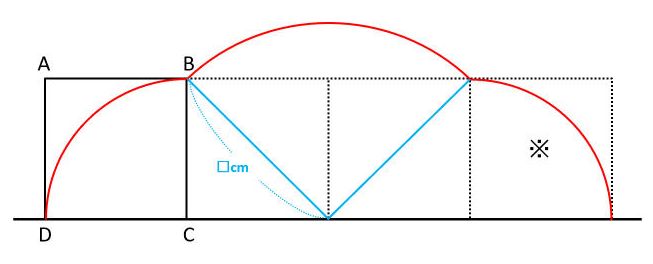
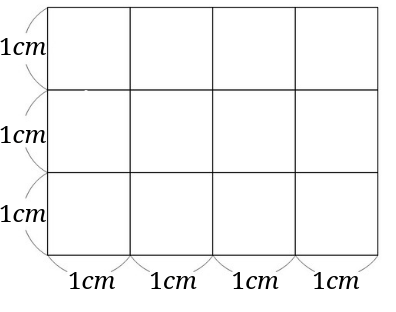
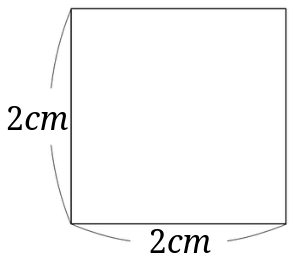
いま、正方形Bの1辺の長さが1cmのとき、正方形Aの1辺の長さを求めてください。 ただし、両側の正方形C、Dは、同じ大きさです。 ※『算法新書』(千葉胤秀(ちば たねひで)編、文政13(10)年刊行)巻の二にある問題です。二等辺三角形の角度の求め方 厳選6問解説! 正三角形の角度 正方形、ひし形との融合問題を解説! 平行四辺形とひし形の違いってなに?? 平行四辺形の角度、辺の長さを求める問題を解説! 平行四辺形の中から面積の等しい三角形を見つける問題を徹底314×1=314 314×2=628 314×3=942 314×4=1256 314×5=157 314×6=14 314×7=2198 314×8=2512 314×9=26




一辺の長さが8 である正方形がある 面積がこの正方形の2倍となる正方形の一辺の長さを Clear



小学6年生の面積の問題です 求め方がわからないので 教えてください よ Yahoo 知恵袋
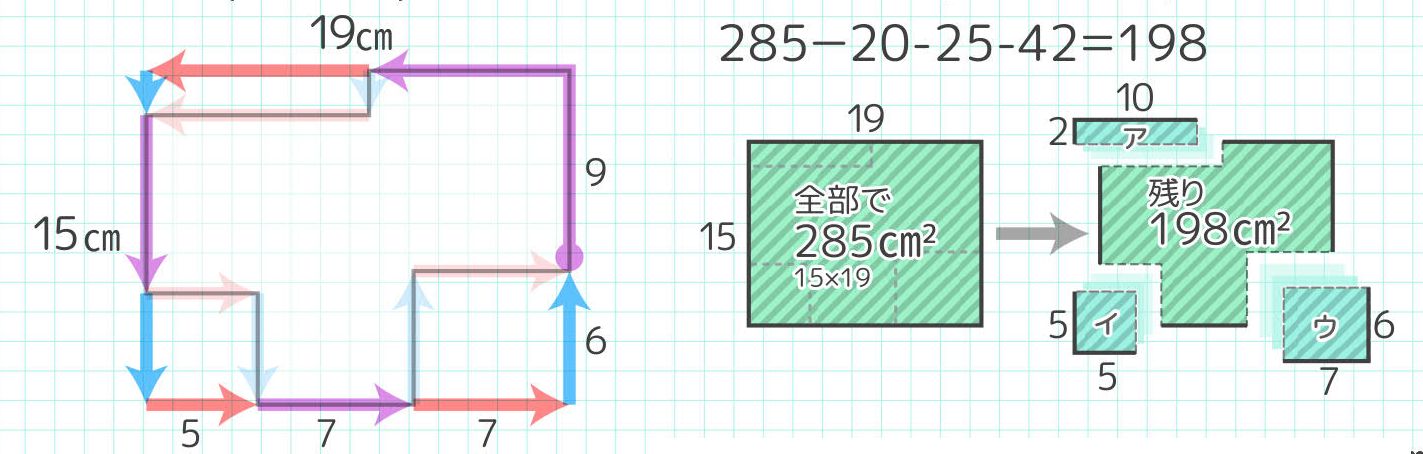
グリッドは空間表現の基本ツールですので、是非とも描き方をマスターしたいところです。 グリッドの何が便利かというと、マス目が物差しとして機能することです。 上図の場合、正方形の一辺は25cmを想定しています。 グリッドのマスを目盛りとして使えば、図中に描かれた机の寸法は幅50cm×奥行75cm×高さ60cm程度であることが読み取れます。 本サイトでは、各求め方はいろいろありますが,正方形全体からよけいな三角形をひいていくのが,ごくふつうの解き方でしょう。 (cm 2) (cm 2) (cm 2) (cm 2) 三角形ABC =正方形全体-(ア+イ+ウ) =36-(15+6+2) =13 (cm 2) 答え 正方形 対角線 の 求め 方三平方の定理を応用すると、正三角形の高さを求めることができる。 例題 右の図のような正三角形の高さ h を求めよ。 (解法) 正三角形 abc の頂点aから底辺bcに垂線ahをおろすと、図のように、点hはbcの中点になる。



小2から プリント12枚 正方形長方形の面積の求め方と公式 対角線からも 中学受験まで そうちゃ式 受験算数 2号館 図形 速さ




正方形をナナメにすると アセント学習塾 塾長の こうかい 日誌
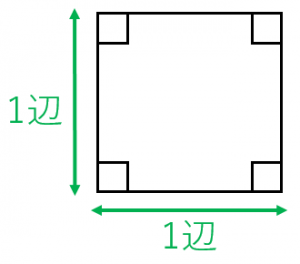
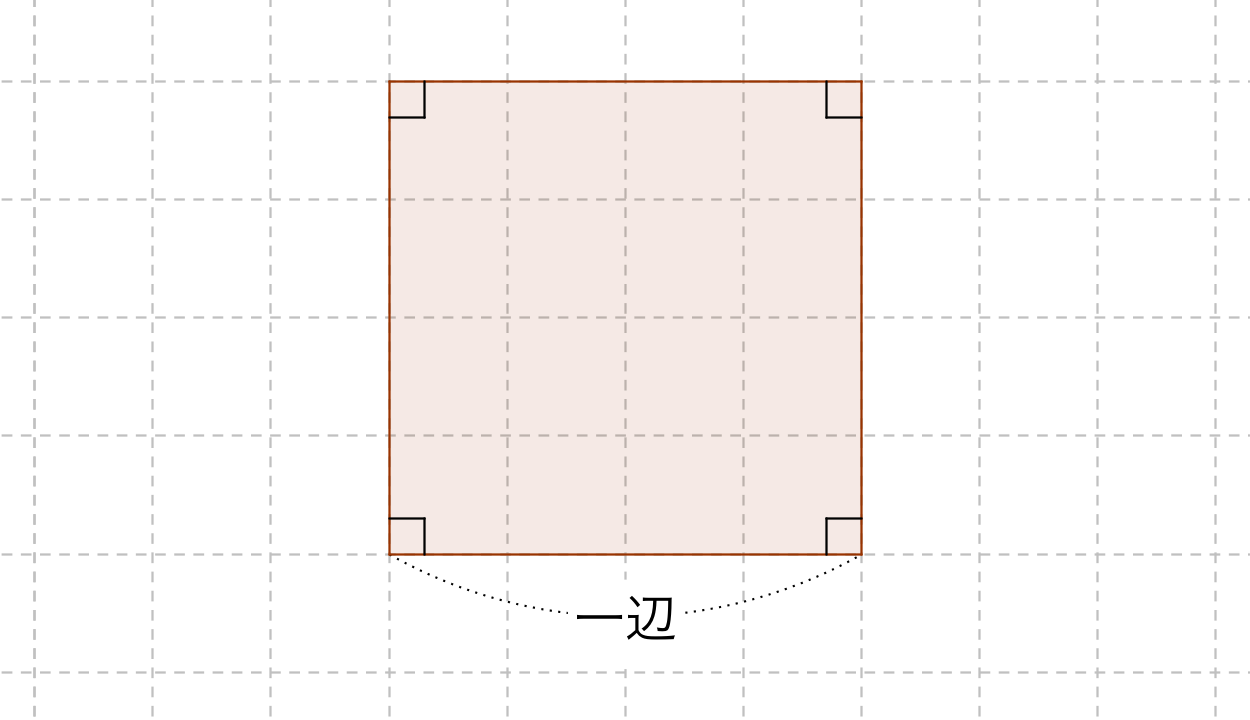
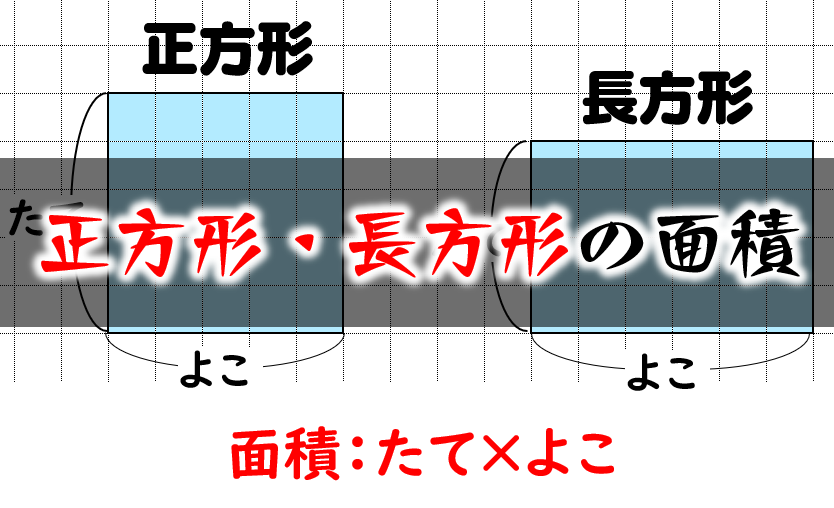
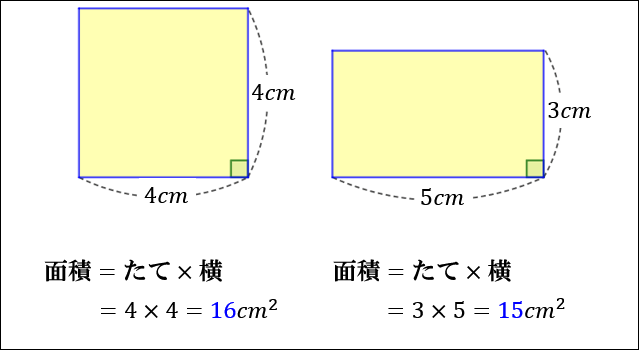
正方形・長方形の面積の公式 正方形と長方形はどちらも面積は 『たて×よこ』 で求めることができます。 たとえば以下のような問題の場合。 例題 「たて・よこ 5cm 5 c m の正方形」と「たて 4cm 4 c m ・よこ 6cm 6 c m の長方形」の面積をそれぞれ求めよ。 それぞれの面積はこのように計算できます。 正方形の面積 : 5× 5=25(cm2) 5 × 5 = 25 ( c m 2) 長方形の面積 : 4× 6 正方形コイルを磁束密度bの領域に通させる問題です。物理が得意な方お願いします。 画像の縦枠で区切られた範囲には磁束密度bが図の記す向きに働いています。 この中に1辺がlの正方形コイルを一定の速度vで通します。 コイルの全抵抗はrとします。 1cm方眼を利用して面積が3,6,7平方センチメートルの正方形の作り方を教えてください!!コンパスを使っていいなら簡単で, いずれも「その正方形の辺の長さをどのように求めるか」という勝負になります1 3cm^2 の場合1 直径が (31)=




簡単公式 正方形の対角線の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




ひし形の面積の公式 面積の求め方は対角線に注目しよう 中学や高校の数学の計算問題
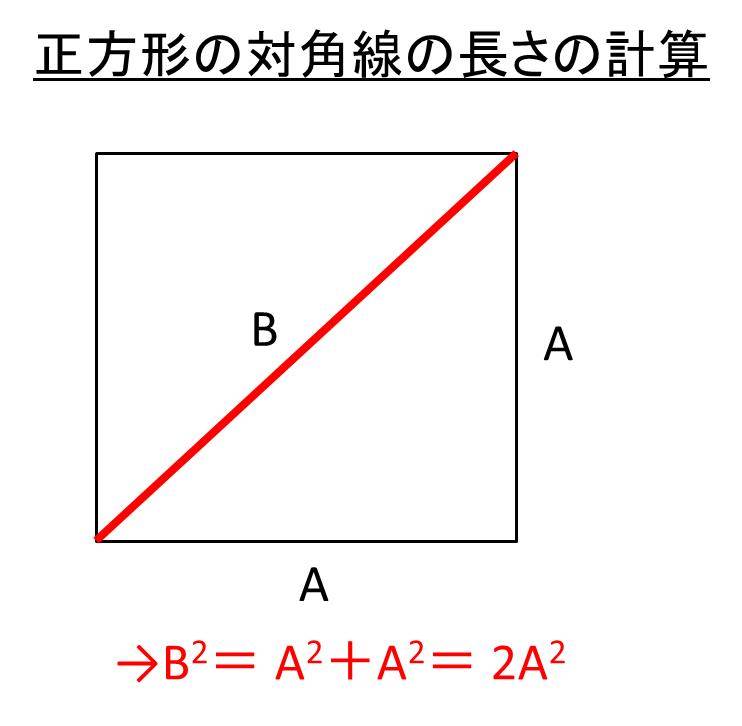
内側の正方形 (ひし形)水色の部分の面積を考えさせます 下の図から、水色の正方形 (ひし形)は、1辺が10cmの正方形が2つ分になることを気づかせます 下の水色の直角三角形を上の濃い水色のところに移動すると正方形2つ分の面積になります。正方形は全ての辺が等しく、隣り合う辺のなす角度が直角です。 正方形に対角線を引くとき2つの三角形ができます。 この三角形の斜辺をピタゴラスの定理で算定すると141Lが算定できます。 今回は正方形の対角線の値、公式、長さの計算、辺の長さとの関係について説明します。 正方形の面積の求め方は下記が参考になります。 正方形の面積は? 1分でわかる(1)1辺の長さが10㎝の正三角形の面積を求めなさい。 (2)次の図形の面積を求めなさい。 3右の図のように,半径6㎝の円Oで,弦ABの長さが 8㎝のとき,円の中心と弦ABとの距離を求めなさい。 (図を一部変えました。) 10㎝ 12㎝ 7㎝ 5㎝ 60° ㎝ χ㎝ y㎝



長方形の周の長さ



教育ソフト開発研究所 5年5巻
1 12 モニタ 単位数算出 の計算式 正方形 および 矩形照射野 における MU 値を求めるための 、一般的 な式を下記 に示す ここで MU モニタ 単位数 (MU 値) D (d,s ) 深さd,照射野 s,の線量評価点 に対して 処方 された 線量 (cGy) DMU 基準深 の線量率 (cGy/MU) Sc(c) 上下絞 り開度 に対する 等価正(求め方①) (求め方②) おうぎ形の中心角をx とすると, おうぎ形の弧の長さは,底面の 円周の長さに等しく,8πcm。 また,半径が12cmの円周の長 これを解いて,x =1 さは,24πcm。 よって,求める側面積は, よって,求める側面積は, 222正四面体の6つの辺の長さは等しく、これを a とします。正四面体の体積は、次の式で求まります。 正四面体 (せいしめんたい) の体積 \begin{align*} V = \frac{\sqrt{2}}{12}a^3 \end{align*} 体積 = 141 × 一辺 × 一辺 × 一辺 ÷ 12




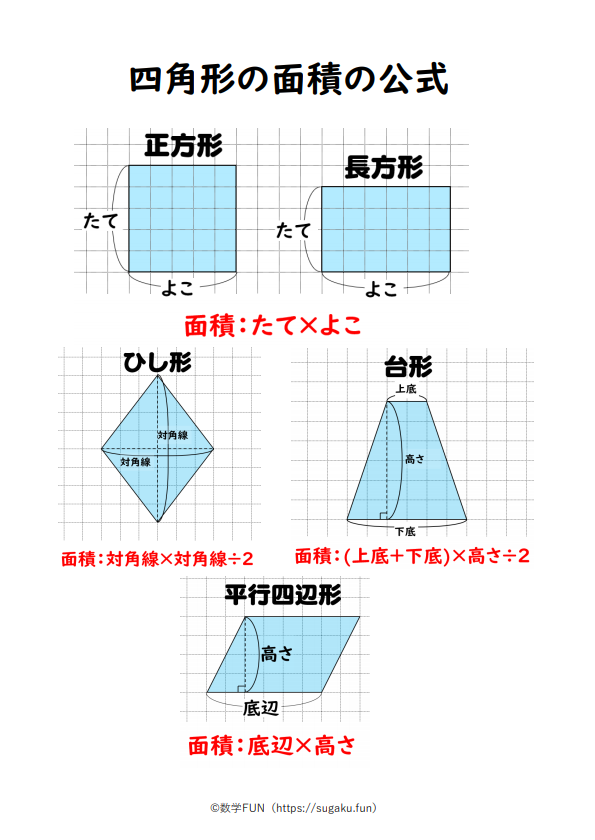
四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




正方形面積公式 正方形 面積の計算 計算 Rtndn
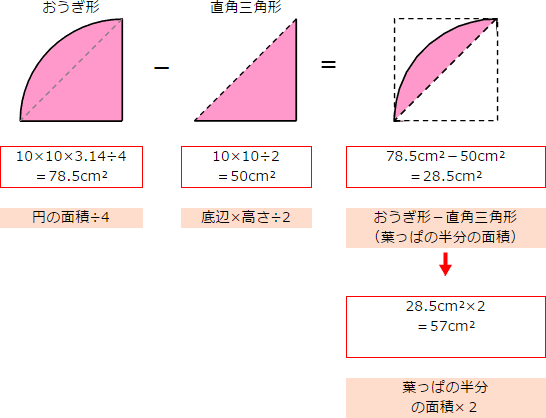
4年算数 大きい面積の求め方 子どもの学習支援 by いっちに算数 スマホ版 前のページに戻る 教え方4 平方メートル の単位を教え、平方メートル と平方センチメートル の単位の関係に気づかせます。 そのあとで、㎝とmの単位を混合した正方形や長方形の面積を求める問題を考えさせます。正八角形の中に二等辺三角形が8つ分できてることに気が付きますね。 なので、 二等辺三角形の面積を求めて、それを8つ分にする。 という考え方で正八角形の面積を求めていきます。 中心の360°を8等分していることから おうぎ形の面積(等積移動系)を求めよ問題のパターン 1 等積移動:同じ面積の所に移動させて計算しやすくする 2 葉っぱ4枚:小さい正方形4つに分ける(正方形の面積×057) 3 補助線+等積移動:補助線を引いて等積移動する 4 ヒポクラテスの三日月



三平方の定理 正方形の対角線を求める Youtube
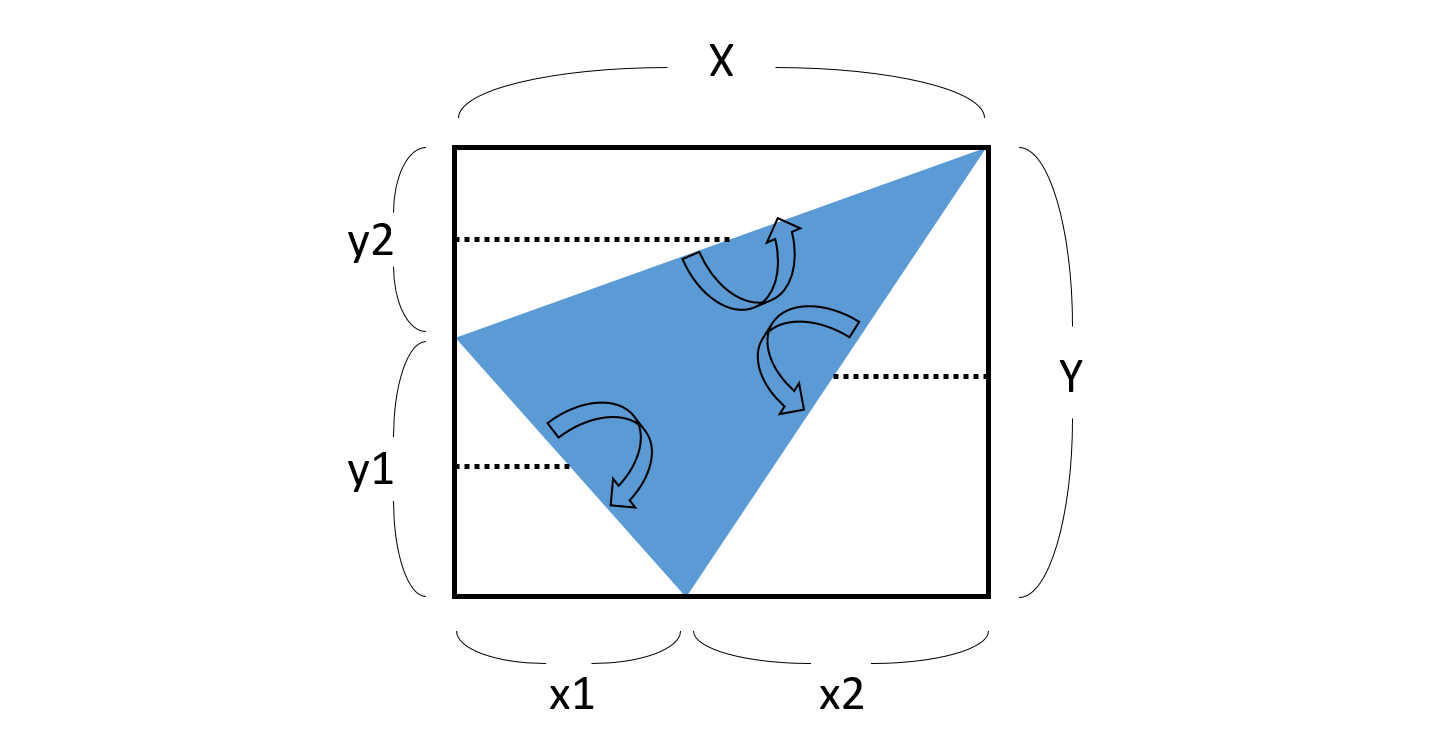



正方形の中にある三角形の面積の平均の求め方 三角形を分解して組み立てなおす Musyokutoumei
A の面積だけの求め方を考える! a の部分の面積を求めるには左図の手順でよい! (扇形の面積)=π(10) 2 (100/6)π (正三角形の面積 (残りの部分)=(100/6)π- (扇形30゜の面積)=π(10) 2 (100/12)π (残りの部分)=(100/6)π- (a部分)=(100/12)π-(100/6)π-) = χ=(正方形)-(a+b+c+d) ) = = cm 2 以前、こ
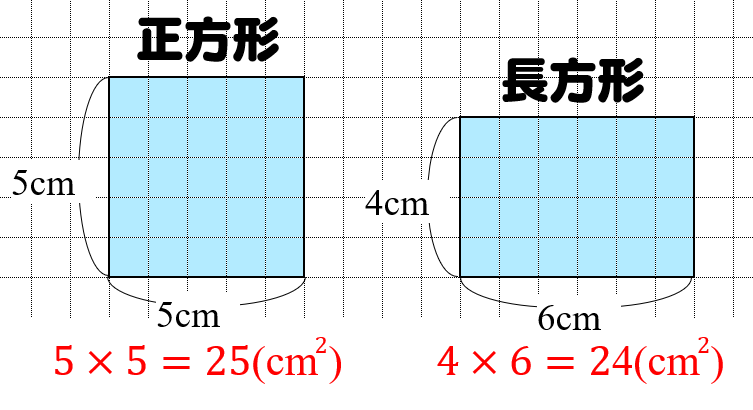



正方形 長方形の面積の求め方 小学生に教えるための分かりやすい解説 数学fun




簡単公式 正方形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく




体積の求め方 計算公式一覧



正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ
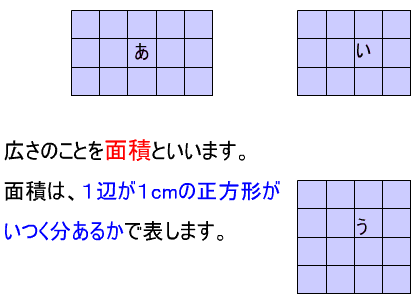



長方形の面積を求める公式の数学的な意味 Note Board
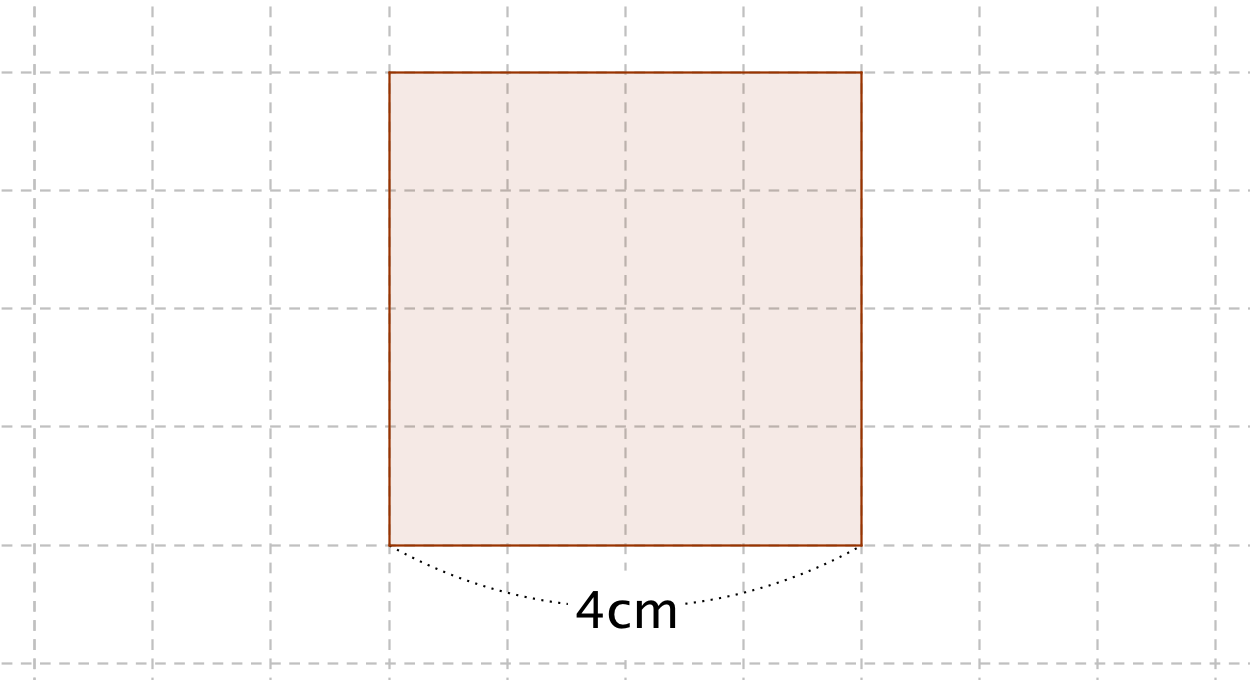



正方形の面積の公式 算数の公式



正方形と長方形の面積 家庭学習レシピ



4年算数大きい面積の求め方わかる教え方
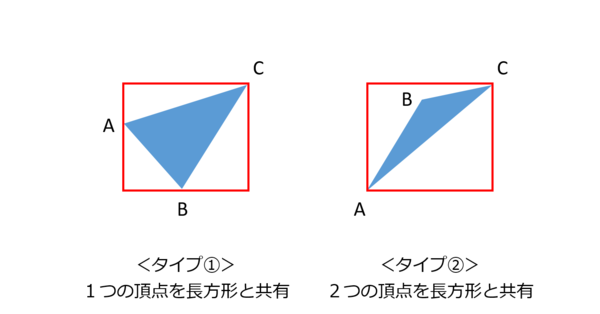



正方形の中にある三角形の面積の平均の求め方 三角形を分解して組み立てなおす Musyokutoumei



正方形の面積は 1分でわかる公式 対角線 ルートの関係 面積から辺の長さを求める方法



1




正方形の求め方を解説みてもわからないのでおしえてほしいです Clear



正方形になる時のpの座標の求め方教えてください 至急お願い致しま Yahoo 知恵袋



簡単公式 正方形の対角線の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




正方形の面積の求め方 小学生の子でもできるチョー簡単な問題 中学や高校の数学の計算問題



簡単公式 対角線で正方形の面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく




19 座標平面上の正方形の問題 Youtube



三つの正方形の合計面積の求め方を教えて下さい 例えば小さい正方形の一 Yahoo 知恵袋



正方形の面積を求める2つの公式 具体例で学ぶ数学



正方形の求め方問題 移り気



正方形の対角線の求め方と対角線から辺の長さを計算する方法 モッカイ




標準 おうぎ形と正方形の面積 なかけんの数学ノート
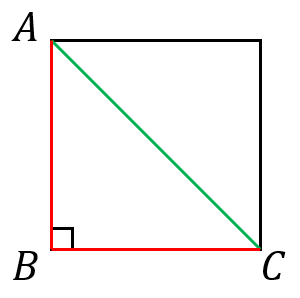



正方形の対角線の長さを求める方法 具体例で学ぶ数学



正方形の対角線の求め方と対角線から辺の長さを計算する方法 モッカイ




対角線 公式 正方形




中学受験 算数 正方形の対角線の長さ 中高一貫 適性検査解説 Note
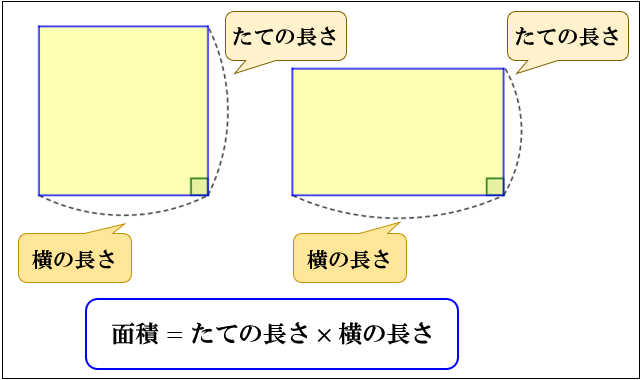



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
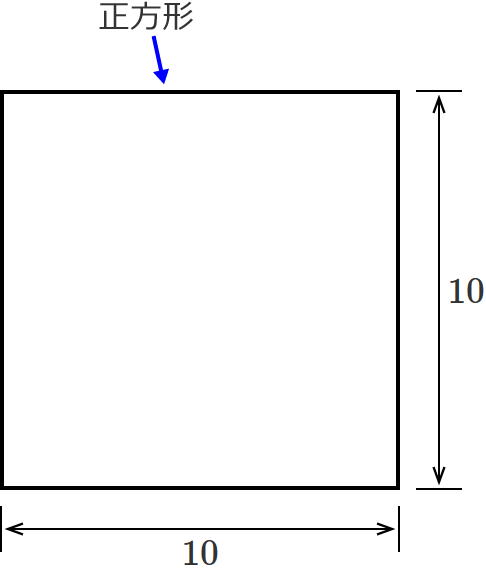



正方形の対角線の長さの求め方



正方形や長方形の面積の求め方は 小学生は公式を覚えないとだめなの みけねこ小学校



正方形の求め方問題 移り気



正方形や長方形の面積の求め方は 小学生は公式を覚えないとだめなの みけねこ小学校




公式なんて覚えない ひし形の面積は直感的に考えよう
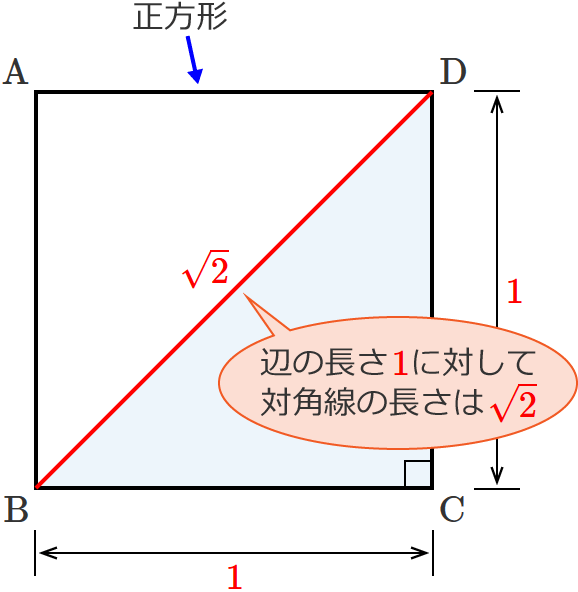



正方形の対角線の長さの求め方
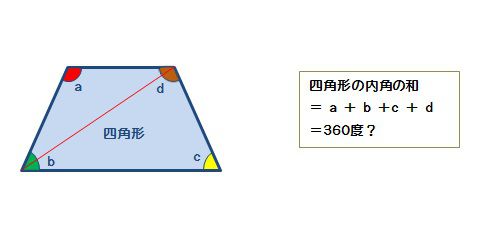



四角形の内角の和 算数の公式覚えてますか



正方形や長方形の面積の求め方は 小学生は公式を覚えないとだめなの みけねこ小学校



正方形の面積の公式 算数の公式



正方形 対角線 長さ 求め方 小学生 6411 正方形 対角線 長さ 求め方 小学生 Wow Top



正方形 長方形の面積の求め方 小学生に教えるための分かりやすい解説 数学fun



正方形の面積を求める2つの公式 具体例で学ぶ数学




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun



面積 上 面積の意味から 正方形 長方形 平行四辺形 三角形の面積の求め方までの通販はau Pay マーケット 学参ドットコム
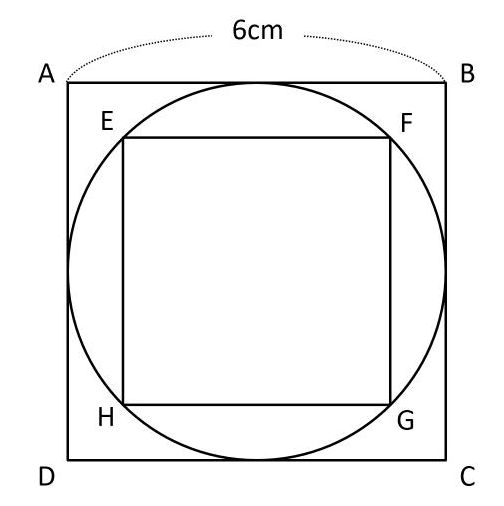



正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ



1



ベクトルの回転 正方形の中心を考えた求め方 Nobumassa Visione



1
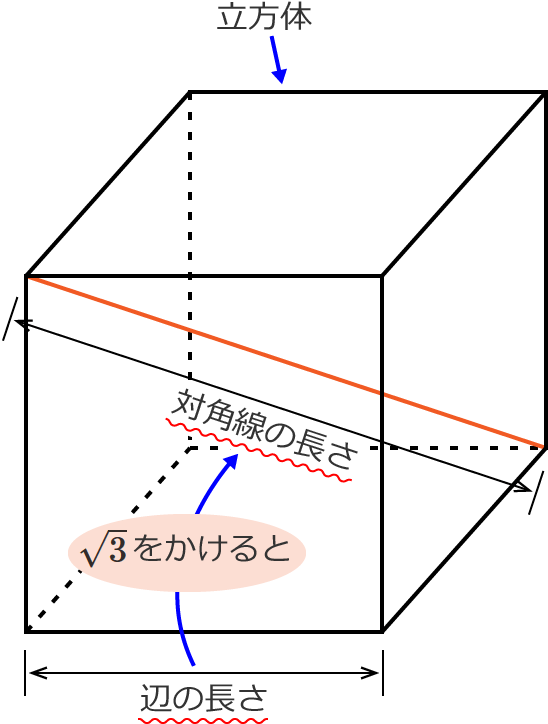



立方体の対角線の長さの求め方



正方形 の 面積 の 求め 方 正方形の面積は 1分でわかる公式 対角線 ルートの関係 面積から辺の長さを求める方法 Amp Petmd Com




5年算数面積 教え方のポイント




簡単公式 対角線で正方形の面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく




標準 おうぎ形と正方形の面積 なかけんの数学ノート



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ




小6算数 円の面積 指導アイデア 2 みんなの教育技術




標準 おうぎ形と正方形の面積 なかけんの数学ノート
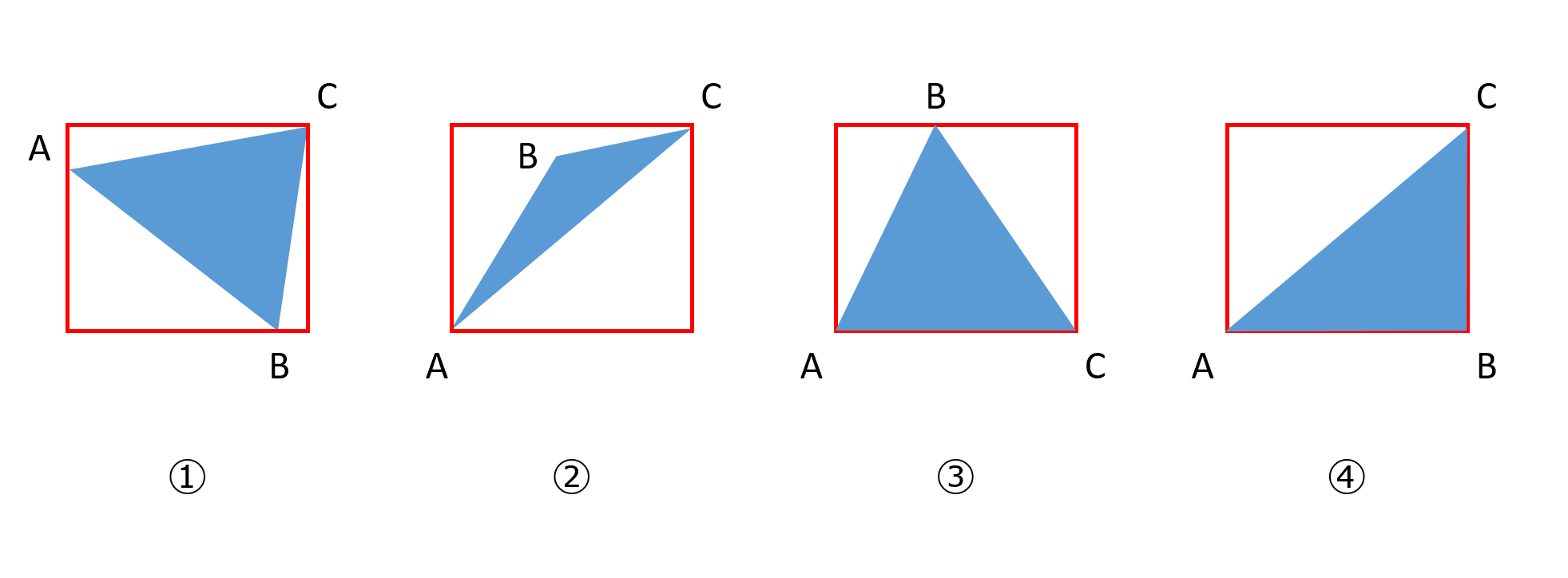



正方形の中にある三角形の面積の平均の求め方 三角形を2つのタイプに分ける Musyokutoumei



正方形の面積は 1分でわかる公式 対角線 ルートの関係 面積から辺の長さを求める方法



正方形 の 面積 の 求め 方 正方形の面積は 1分でわかる公式 対角線 ルートの関係 面積から辺の長さを求める方法 Amp Petmd Com
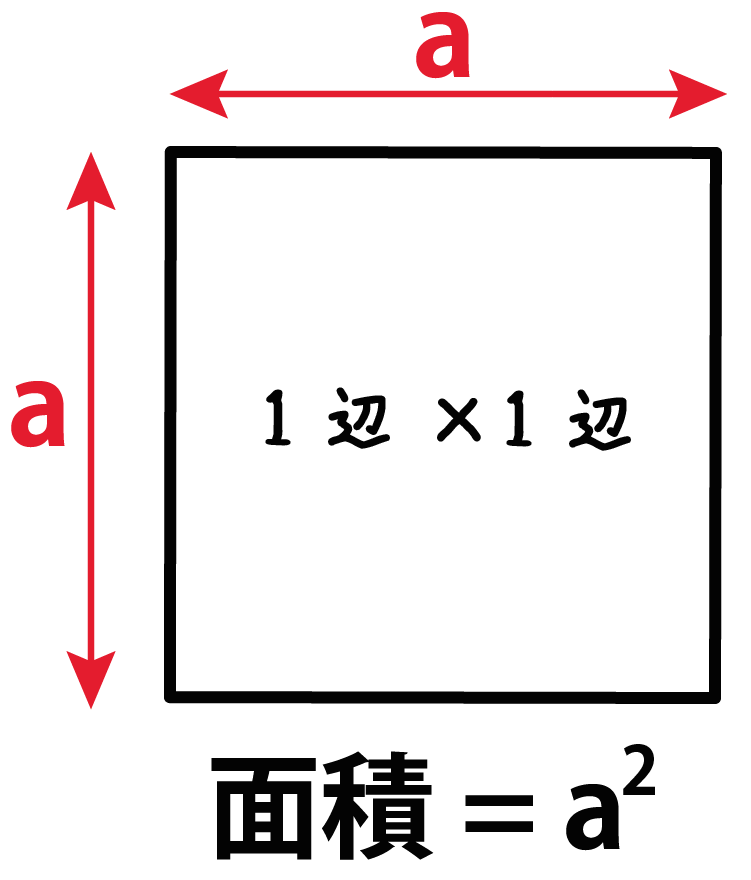



簡単公式 正方形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく




平成27年度算数教科書読み比べ 8 円の面積の求め方 わさっきhb




Asahi Com 朝日新聞社 面積の不思議 おーっ 花まる先生公開授業 教育




対角線 長さ 長方形



フェイス 遠賀 フェイス777遠賀 Amp Petmd Com




正方形や長方形の面積の求め方は 小学生は公式を覚えないとだめなの みけねこ小学校




図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト
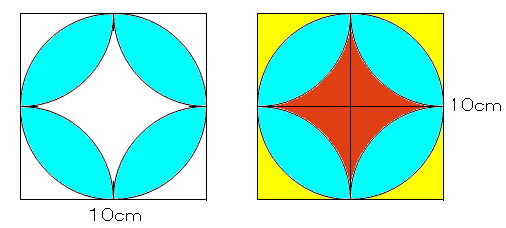



算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素




正方形の面積 高精度計算サイト



1




円の面積 算数用語集
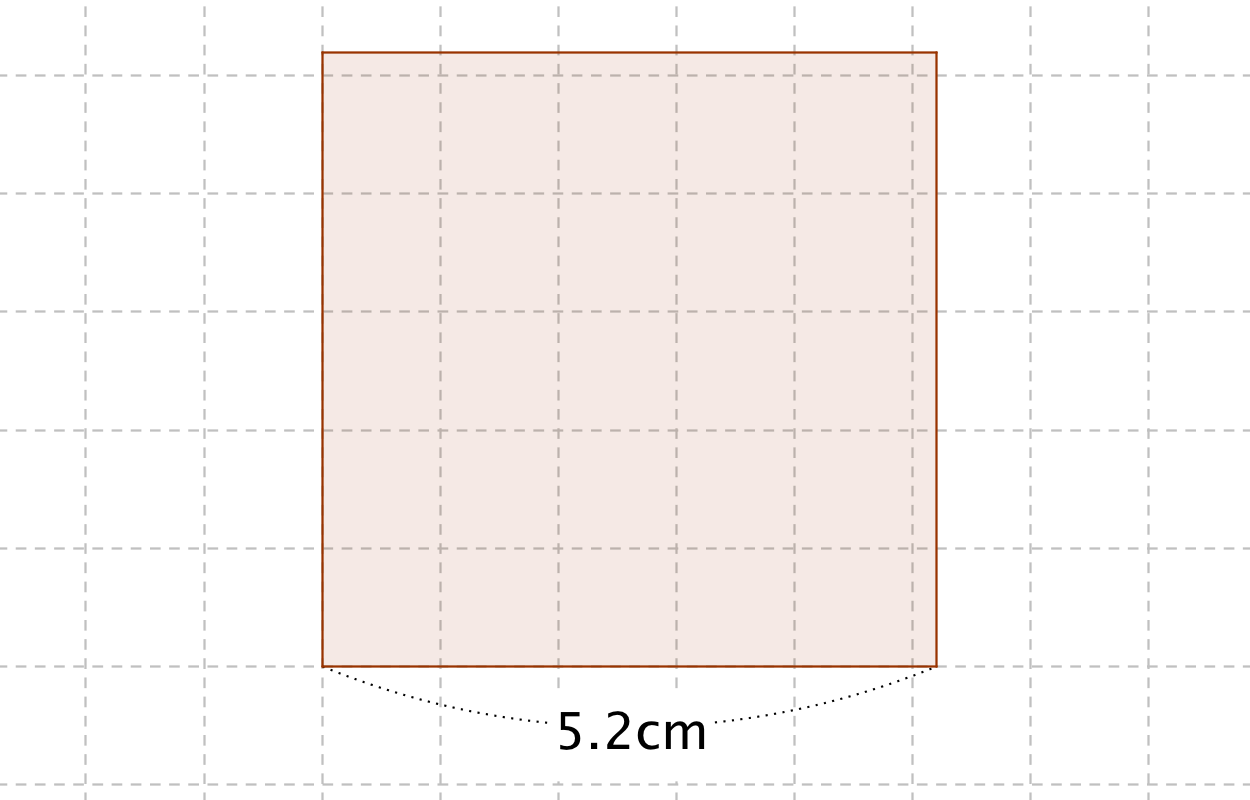



正方形の面積の公式 算数の公式




簡単公式 正方形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく




正方形の対角線の求め方と対角線から辺の長さを計算する方法 モッカイ




面積の求め方を教えて頂きたいです Clear




正方形 長方形の面積の求め方 小学生に教えるための分かりやすい解説 数学fun




正方形の対角線で面積を求めることができる 知らない人も多いぞ 中学や高校の数学の計算問題




数学の図形の面積についてです 画像の色のついた部分の面積の求め方 数学 教えて Goo



Laf先生 正方形の対角線の求め方 中3数学 平方根の利用 Powered By Line



4年生 10 長方形と正方形の面積の求め方 Youtube
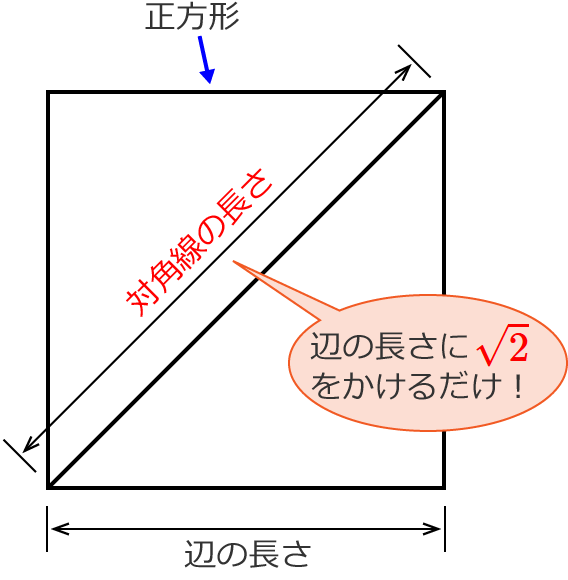



正方形の対角線の長さの求め方
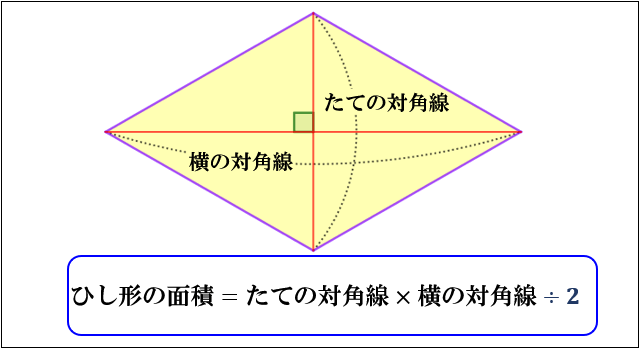



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



正方形の対角線は 1分でわかる値 公式 長さの計算 辺の長さとの関係



H21面積




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
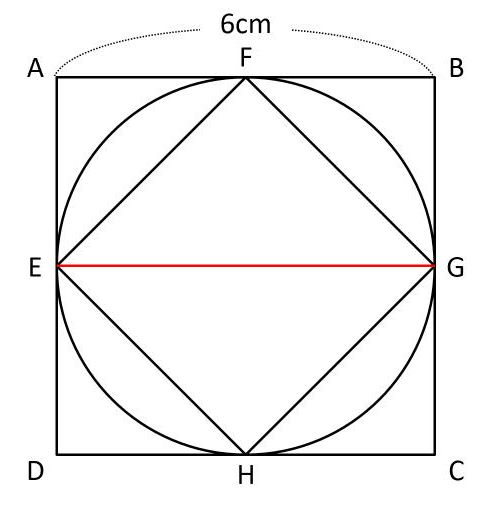



正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ
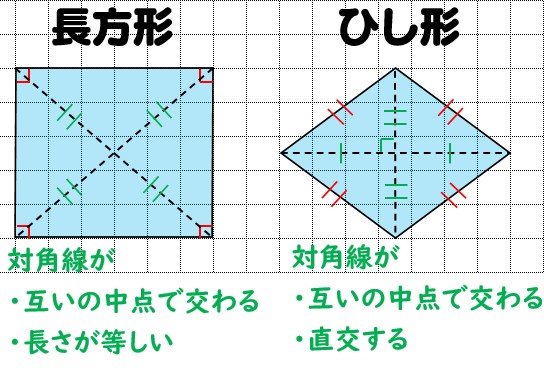



対角線の求め方 小学生




正方形の面積の求め方 小学生に教えて下さい Youtube
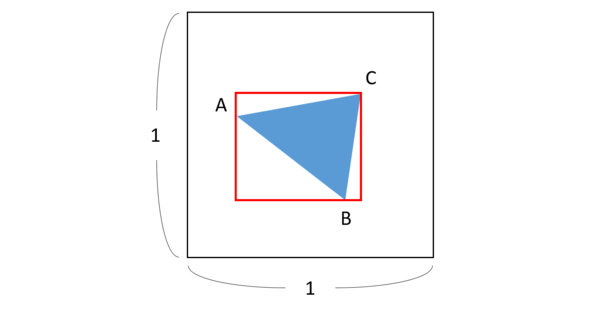



正方形の中にある三角形の面積の平均の求め方 三角形を囲む長方形の面積 Musyokutoumei
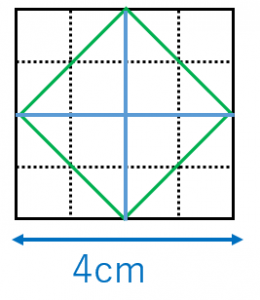



正方形の面積を求める2つの公式 具体例で学ぶ数学




4 2 長方形 正方形の面積 算数がわかるようになるページ



面積の求め方 算数の教え上手 学びの場 Com



対角線 公式 正方形


